施益烽  魏婷

南京晓庄学院教师教育学院

电邮：{2572953755, 68120886}@qq.com

【摘要】 目前，计算思维的培养呈现出“低龄化”、“跨学科”的趋势。小学STEM课程作为跨学科实践的重要形式，承担着培养小学生计算思维的重要任务。研究对小学开设的STEM课程进行了调研，并对STEM课程下小学生的计算思维发展现状进行了分析，提出小学生计算思维发展策略。

【关键词】 计算思维、STEM课程、小学生

Abstract: Nowadays, the cultivation of computational thinking shows a trend of younger age and interdisciplinary. As an important form of interdisciplinary practice, STEM courses in primary schools undertake a important task of cultivating students’ computational thinking. Our research conducted a survey of STEM courses offered by primary school, and analyzed the development status of students’ computational thinking in primary schools based on STEM courses, last but not least, we put forward some strategies of developing computational thinking of primary school students.

Keywords: Computational thinking, STEM courses, Primary school students

1.前言

随着互联网技术的高速发展，信息技术与教育的结合越来越紧密，信息技术不再是单纯的教学辅助手段，它渗透在教育的方方面面，与不同学科紧密融合。在这种学科融合的大背景下，计算思维作为信息技术的核心素养，其培养方式也不再局限于编程，而是更加注重在跨学科的复杂情境中利用信息技术来解决问题。同时，随着人工智能在中小学的逐步普及，小学生有更多的机会接触STEM课程。不同于小学其他的综合类课程，STEM课程更加注重“跨学科”、“复杂情境”等因素，这些因素十分契合小学生计算思维的培养。此外，美国的《K12计算机科学框架》也提倡基于STEM课程来培养学生的计算思维。因此，探索STEM课程中小学生计算思维发展的现状，可以为后续在STEM课程中培养小学生计算思维提供事实参考依据。

2.计算思维：数字时代的一种问题解决能力

21世纪以来，全球进入了数字化发展的快车道，计算机科学领域的相关技术广泛应用于生活的各个方面，其中的各种思想方法也在不断地与我们的生活发生碰撞。计算思维作为人类的三大科学思维方式之一，开始逐渐摆脱专业学科的束缚，成为一种数字时代普遍适用的问题解决能力。

周以真教授认为，计算思维是一种求解问题的方法，是人独有的，并不是计算机的思维方式。计算思维以设计和构造为特征，在数学思维的基础上，融合了工程思考。她将计算思维定义为运用计算机科学的基础概念进行问题求解、系统设计、以及人类行为理解等涵盖计算机科学之广度的一系列思维活动(Wing, J. M,2006)。

国际教育技术协会（ISTE）和计算机科学教师协会（CSTA）将计算思维定义为一个问题解决的过程，其特点为：拟定问题（该问题适合用信息技术来解决）；数据的整理和分析符合逻辑；通过抽象等手段，实现数据的可视化；借助算法，实现问题解决的自动化；分析并寻找最有效的方案；将解决问题的过程迁移到其他问题上(Seehorn, Deborah, Carey, Stephen, Fuschetto, & Brian, et al,2011)。

任友群 (任友群，隋丰蔚和李锋,2016)等人在分析大量已有的研究成果上，给出了自己对计算思维的理解：计算思维是一种蕴涵了计算机科学基本思想方法的问题解决过程。凭借计算思维，人们可以更有效的分解问题，建立模型，采用模块化，自动化，系统化的方式解决问题。

2017版《普通高中信息技术课程标准》(中华人民共和国教育部,2017)将计算思维定义为个体运用计算机科学领域的思想方法，在形成问题解决方案的过程中产生的一系列思维活动。该定义在《义务教育阶段信息技术课程标准》中同样适用。

综上所述，计算思维并不是伴随着计算机科学而诞生的，但是计算机的出现凸显了计算思维的重要性；同时，计算思维不仅仅是强调信息技术的使用，计算思维更加重视将计算机科学领域的思想方法引入到日常生活中，用以解决实际问题。

3.STEM课程：基于项目的跨学科学习

3.1.STEM课程定义

STEM是科学（Science）、技术（Technology）、工程（Engineering）和数学（Mathematics）四门学科的简称，强调跨学科、学科之间的融合。STEM课程不是简单的将科学、技术、工程、数学类课程糅合到一起，而是要根据实际情况，在这些学科之间建立起联系，形成一个有机的整体，学生在这种课程上，交叉运用不同领域的知识解决问题。

沙欣(Sahin, & Alpaslan,2015)将STEM课程定义为一种体验式课程，教师引导学生在项目活动中运用跨学科的知识，通过合作的方式设计、建构、发现和解决问题。董泽华(董泽华,2016)认为，STEM课程不同于传统的分科课程，其具有项目驱动、学习共同体、知识整合、协同教学、实践应用、跨界资源聚合等特殊性。余胜泉(余胜泉和胡翔,2015)指出，STEM课程应具有以下特征：跨学科、趣味性、体验性、情境性、协作性、设计性、艺术性、实证性和技术增强性等。在这种整合性的课程下，学生能够无视学科壁垒进行思考，在掌握知识和技能的同时，又可以将解决问题的思想方法迁移到现实生活中，培养应用意识。赫希巴奇(Herschbach D R,2016)认为，STEM课程是一种广域的课程模式，它不再强调科学、技术、工程和数学等学科的独立存在，而是要打破学科之间的界限，通过活动将各种课程整合成结构化的课程模式。

综上所述，STEM课程是一种整合性课程，将科学、技术、工程和数学学科中零散的知识通过项目活动联系起来，整合成一个具有逻辑结构的学习情境，在这种学习情境中，教师引导学生运用“无学科壁垒”的眼光发现问题，交叉运用不同学科的知识解决问题。

3.2.小学STEM课程开设现状

研究对南京、无锡、连云港地区13所小学进行了走访调研，对27名不同学科的小学教师进行了访谈，发现：小学开设的STEM课程大都融入在信息技术、科学等综合类课程中，或者是以校本课程、社团课程等研究性课程的形式开展，还没有形成系统的课程体系。从课程的类别来看（见表1），主要包括以下几类：设计类、编程类、动手类、游戏类。其中，设计类的课程主要包括：科学实验设计、实践活动设计等，这类课程要求学生在综合运用科学、数学、计算机科学等学科知识的基础上，辅以工程思维，完成项目的设计；编程类课程主要包括：计算机程序设计、机器人编程等，这类课程要求学生运用多学科的知识设计和综合问题的解决方案，并利用算法来实现；动手类的课程主要包括：手工制作、航模、3D打印等，这类课程帮助学生形成模型思想，关注学生的动手能力，强调“手脑并用”，充分发挥学生的主动创造性；游戏类课程主要包括：科学小游戏、Scratch编程、数字书画创作等，这类课程注重学生的沉浸式体验，在体验各种游戏的过程中，渗透跨学科的知识。

表 1 STEM课程分类

课程类别	代表性课程	课程特点
设计类	科学实验设计、实践活动设计	跨学科知识+工程思维
编程类	计算机程序设计、机器人编程	跨学科知识+算法思维
动手类	手工制作、航模、3D打印	动手能力+创新思维
游戏类	科学小游戏、Scratch编程、数字书画创作	沉浸式体验+学科知识渗透

4.研究设计与研究对象选择

4.1.问卷的选取与确定

研究选取白雪梅、顾小清(白雪梅和顾小清,2019)所构建的中小学生计算思维量表作为本次测试的评价工具。量表基于Korkmaz等人(Korkmaz O , Cakir R , Ozden M Y,2017)所设计的计算思维量表进行改编，使其适用于我国中小学生计算思维的测评。量表将计算思维分为五个维度，其中，创造力关注学生想法的多样性、思考过程的流畅性、思考结果的创新性；算法思维侧重于考察学生对数据的分析能力以及对模型的归纳总结能力；协作交流主要考察学生的团队合作能力；批判思维关注学生对问题思考与评价的合理性；问题解决能力侧重于对学生分析、处理问题以及解决问题方法的迁移的考察。量表共计20道题：创造力（6题）、算法思维（4题）、协作交流（4题）、批判思维（3题）、问题解决能力（6题）。采用李克特五点法进行计分。

为了检测该计算思维量表是否适用于江苏地区的小学生，在正式测试前，研究对量表的信效度进行了检测。经检验，量表的Cronbach α系数为0.932，其五个维度的Cronbach α系数分别为0.785、0.758、0.863、0.852、0.857，无论是计算思维量表总体还是五个维度，其Cronbach α系数均＞0.7，这表明（见表2），量表信度良好，内部一致性很高。

表 2 计算思维量表信度分析

KMO和巴特利特检验的结果显示（见表3），计算思维量表的KMO = 0.890≥0.8，P = 0.000＜0.05，由Kaiser决策标准可知，Bartlett球形检验达到了显著水平，该量表适合做因子分析。并且，计算思维的各维度也满足该决策标准，表明不同维度下的选项与该维度存在对应关系，量表的框架结构合理。

表 3 计算思维量表效度分析

4.2.研究对象选择与问卷发放

研究按照地区位置选取了江苏省内的无锡（苏南）、南京（苏中）、连云港（苏北）三个城市，采取分层整体随机抽样，将各市学校按所处区域分为城区与非城区。从每个区域中抽取部分小学，包含公办小学和民办小学，在小学的3至6年级随机抽取一定班级进行问卷调查。

问卷以纸质的形式发放，通过班会课、课间等时间，由班级教师督促学生自主完成并回收。共回收到572份问卷，有效率为100%，不同地区、性别和年级学生的样本如表4所示。

表 4 不同地区、性别和年级小学生样本

5.小学生计算思维现状分析：基于STEM课程

5.1.描述性统计

本研究使用SPSS25.0对收集到的数据进行了整理分析，得到了小学生（N=572）计算思维量表的描述性统计分析（见表5）。共20题，其中最高分为100分，最低分为50分，平均得分为79.47分。由此可见，参与调查的小学生计算思维能力尚处于发展阶段。从计算思维的各个维度来看，小学生在各个维度的平均得分依次为：创造力（79.81）、算法思维（78.72）、协作交流（81.97）、批判思维（79.78）、问题解决能力（77.59），由此可见，小学生在计算思维各个维度的发展比较均衡，在现有的课程体系下，小学生的计算思维各个维度的能力均能得到一定的发展。但是对于如何在具体情境中分析问题、将问题模型化、将解决问题的过程自动化，小学生仍需要接受更加系统化、专业化的训练。

表 5 小学生计算思维描述性统计

	N	Min	Max	M±SD	偏度	峰度
计算思维	572	50	100	79.47±12.138	-0.184	-0.868
创造力		33.333	100	79.81±15.0236	-0.511	-0.235
算法思维		30	100	78.72±15.389	-0.417	-0.611
交流协作		20	100	81.97±17.510	-1.048	0.663
批判思维		20	100	79.78±16.655	-0.532	-0.436
问题解决		20	100	77.59±19.239	-0.902	0.379

5.2.性别差异分析

本研究对比男女生的计算思维能力现状发现（见表6），首先，在样本量上，参与调查的女生数量与男性的数量相当，男女比例适宜；其次，从均值上看，男生与女生在计算思维整体上几乎不存在差异；从不同维度看，女生在交流协作维度得分（P=0.049<0.05）较显著高于男生，在批判思维表现上，男生得分（80.66）略高于女生（78.90），但不存在显著差异，其余各维度两者得分均值都相对接近。

表 6 不同性别学生独立样本T检验

5.3.年级差异分析

为了探究不同年级之间的小学生在计算思维上是否有差异，本研究对572名小学生的数据进行了方差分析，结果显示（见表7），从整体上看，不同年级的小学生计算思维能力差异显著（P=0.000<0.05），随着年级的上升小学生的计算思维能力也在不断的发展。从各个维度来看，各年级学生的创造力（P=0.000<0.05）、算法思维（P=0.000<0.05）、交流协作（P=0.033<0.05）、批判思维（P=0.000<0.05）、问题解决（P=0.000<0.05）能力均存在显著差异。这表明了不同年级之间小学生的计算思维差异并不是由单方面原因造成的，而是由其多种认知能力的发展共同影响。

表 7 不同年级小学生计算思维方差分析

	三年级		四年级		五年级		六年级		F	Sig.
	N	M±SD	N	M±SD	N	M±SD	N	M±SD
计算思维	37	67.41± 8.783	263	78.77± 11.717	148	81.22± 11.494	124	82.45± 12.395	17.367	0.000*
创造力		67.39± 17.832		79.18± 14.609		81.036± 13.969		83.38± 14.313	11.904	0.000*
算法思维		67.70± 16.980		77.24± 15.324		80.88± 14.330		82.58± 14.405	11.279	0.000*
交流协作		74.19± 16.688		82.13± 17.021		82.09± 18.608		83.79± 17.005	2.921	0.033*
批判思维		67.43± 14.936		80.10± 15.790		80.74± 16.489		81.65± 17.769	7.764	0.000*
问题解决		61.73± 18.416		75.98± 19.793		81.27± 16.926		81.35± 18.176	13.172	0.000*
*在 0.05 级别（双尾），相关性显著。

STEM课程可以综合发展小学生的多种能力，这当然也包括小学生的创造力、算法思维、交流协作、批判思维、问题解决能力。通过对比不同年级的小学生所接触的STEM课程数量后（见图1），我们发现，有27.03%的三年级小学生没有接触过STEM课程，仅有8.1%的三年级小学生接触过3类及以上的STEM课程；而四年级的小学生仅有7.6%没有接触过STEM课程；五年级的小学生有32.4%接触过3类及以上的STEM课程；接触过3类及以上STEM课程的六年级的小学生占到39.5%。

在对比不同年级小学生计算思维能力差异时，四年级小学生的计算思维较三年级小学生有十分明显的提升，而四年级小学生所接触到STEM课程的机会也远高于三年级小学生，并且随着年级的升高，小学生会接触到更多类型的STEM课程。这表明，随着年级的上升，小学生能接触到的STEM课程数量也越来越多，在不同的STEM课程中，小学生计算思维发展的维度各有侧重，相辅相成，共同促进小学生计算思维的发展。

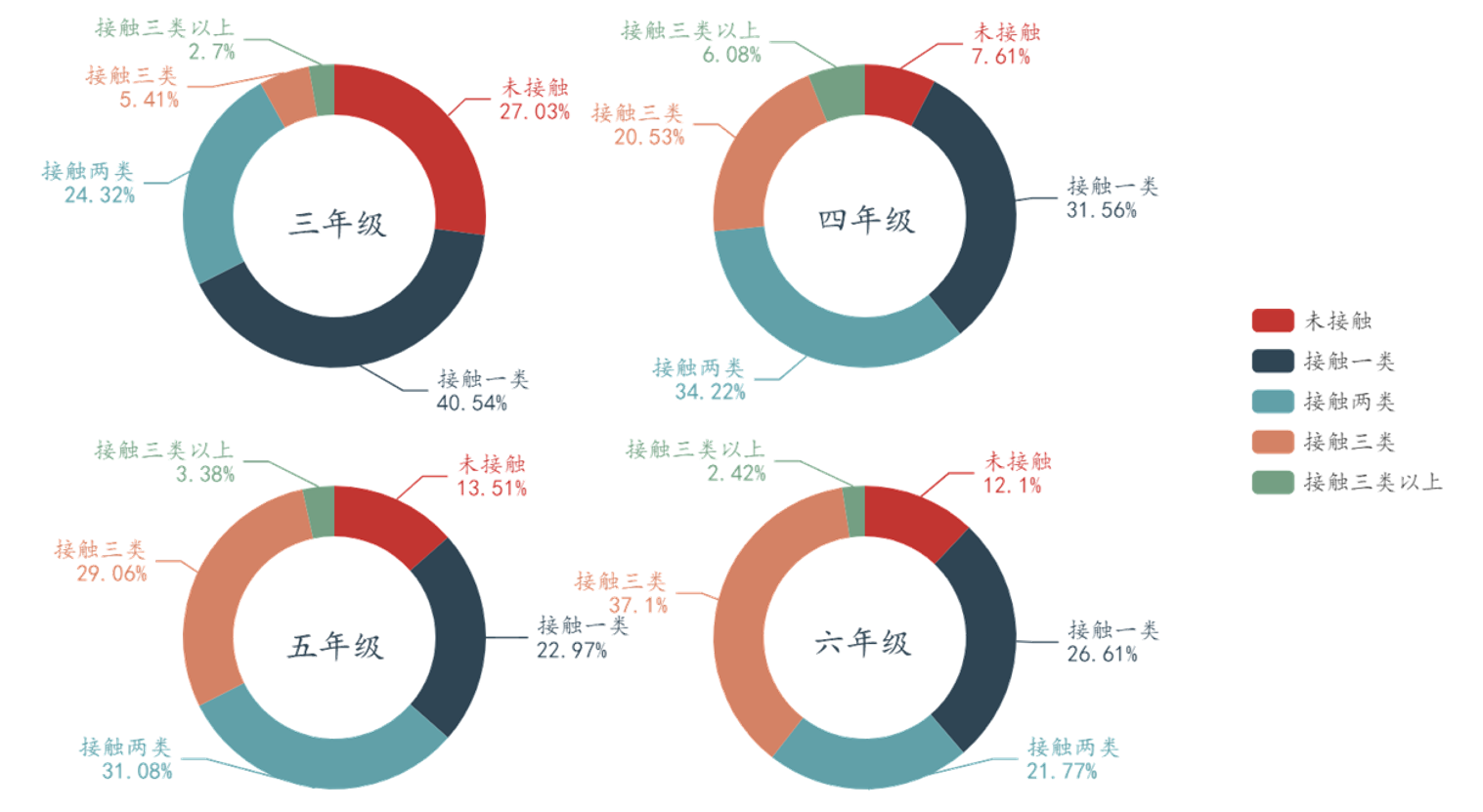
图 1 不同年级学生接触STEM课程数量

5.4.城乡差异分析

研究按照城市区域规划，将所调查的学校分为城区小学和非城区小学，并将城区小学与非城区小学的学生的计算思维进行了单因素ANOVA分析，其结果显示（见表8），城区的小学生与非城区的小学生计算思维差异显著（P=0.025<0.05），城区小学的学生计算思维能力明显强于非城区小学的学生；这种差异主要体现在创造力（P=0.05≤0.05）和算法思维（P=0.012<0.05）上。

表 8 不同地区学生单因素ANOVA分析

研究对不同地区学生所接触的STEM课程类型进行了分析比较。结果显示（见图2），城区的小学生参与编程类以及动手类课程的比例高于非城区的小学生，此外，同时参与编程和动手类课程的城区小学生比例也高于非城区小学生，这说明以程序设计为代表的编程类STEM课程对培养学生的算法思维能力有着重要作用，同时，动手类的STEM课程也有助于学生创造能力的发展，交叉进行多种STEM课程有助于小学生计算思维的提升。

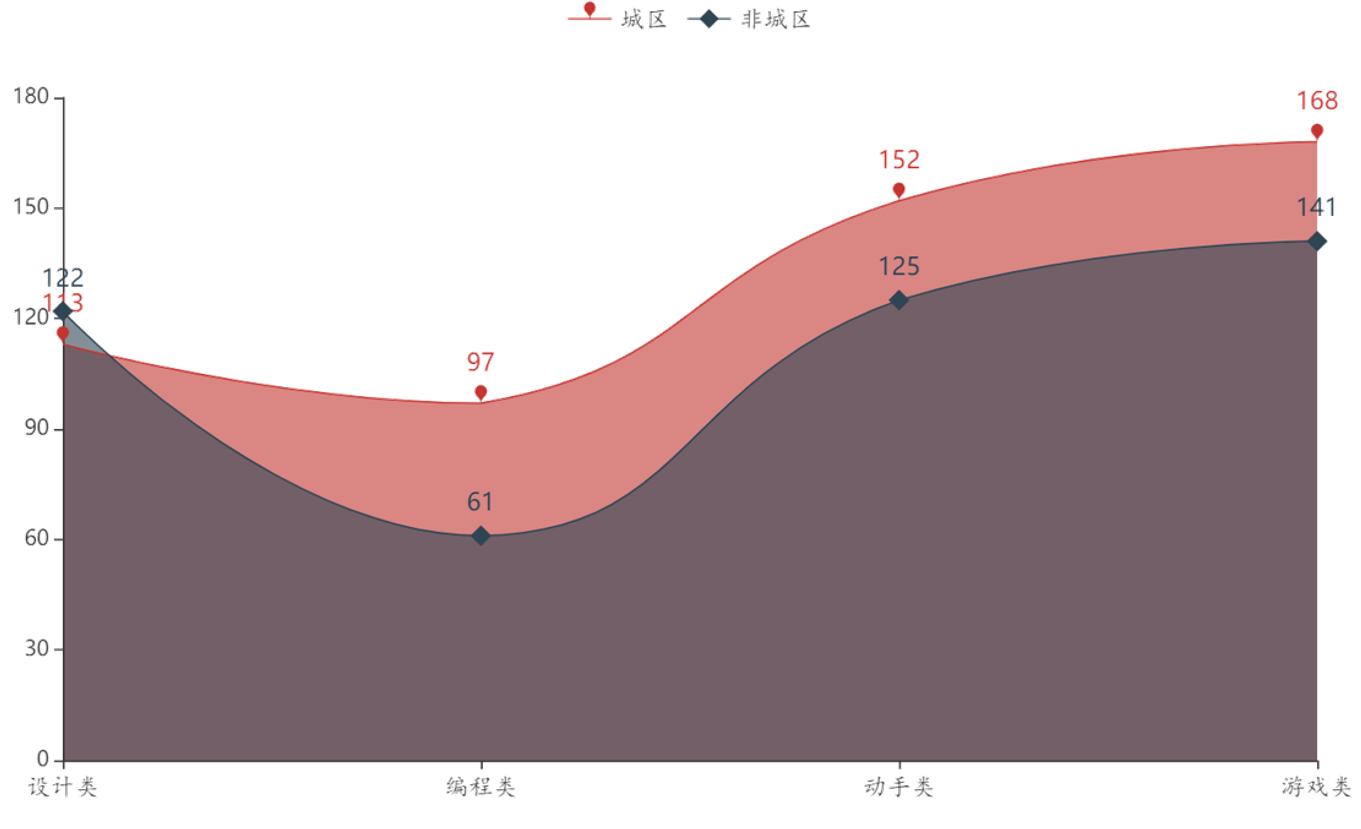
图 2 不同地区学生接触STEM课程类型

5.5.学校类型差异分析

研究所调查的小学中，有不少学校为民办性质的小学，如河西外国语学校、南京外国语学校方山分校等，为了探究民办小学与公办小学的学生在计算思维上的发展状况，将不同的样本分为民办小学组和公办小学组，其学生的计算思维状况如表9所示，民办小学的学生计算思维能力明显强于公办小学的学生（P=0.019<0.05），从计算思维的各个维度来看，除了在问题解决维度，两者的得分均值较为接近外，其余维度上，民办小学的学生都领先于公办小学的学生。这说明，民办小学更加重视对学生各种综合能力的培养，使得民办小学的学生拥有更加出色的计算思维。

表 9 不同类型小学学生计算思维现状

从民办小学与公办小学未参与STEM课程的学生比例上也可以看出（见图3），民办小学的STEM课程普及率要远高于公办小学，民办小学的学生能够更早更全面的接触STEM课程，进而促进其计算思维的培养。

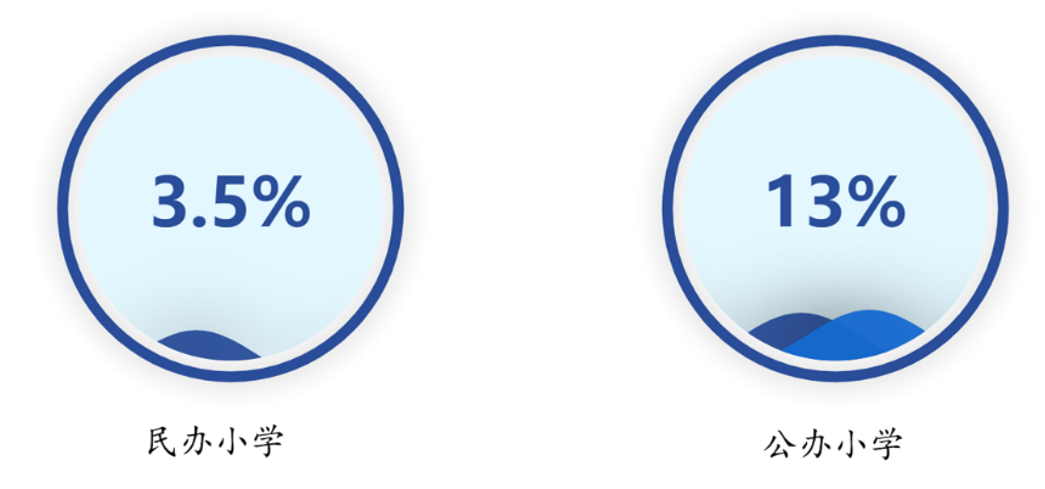
图 3 未参与STEM课程学生比例

6.小学生计算思维发展策略：根植于STEM课程

6.1.学科深度融合，拓宽计算思维发展区间

目前，我国小学生的计算思维培养主要依赖于学校开设的信息技术课程，而信息技术课程虽然和STEM课程有部分交集，但是总体上来说，我国小学的信息技术课程还是作为独立的课程存在的。课程的教学内容一般也是从计算机技术的角度开展，即便涉及到数学、工程等方面的知识，也只是一带而过。学生学习的内容也都以计算机操作为主，很少需要在复杂的系统环境下思考和解决问题。因此，信息技术的教学需要加深与其他学科的整合，通过STEM为学生提供更加丰富的知识，构建更加真实的学习环境，使每一个学生都有机会参与，在“真实环境”中发挥计算思维，发展计算思维，从而提升核心素养。

6.2.开设类别多样的STEM课程，均衡发展计算思维

计算思维的好坏会受到多种能力的影响，发展计算思维也不能停留在单一的维度上。不同的STEM课程对小学生能力的发展也各有侧重，例如，在机器人编程的课程中，整个项目会涉及到机器人的搭建、程序的编写、实际调试等环节，包含了创造力、算法思维、协作交流、批判思维、问题解决等多种能力的培养。但是课程的核心内容还是编程和调试，机器人的搭建大部分还是依据图纸按部就班的完成，对学生动手创造能力的发展并不明显，长此以往，就容易造成小学生个体内部计算思维发展的不平衡。因此，开设类别多样的STEM课程对平衡小学生计算思维的发展就显得尤为重要，通过各有侧重的不同课程，可以协调计算思维各个维度的发展状况，形成完整的计算思维培养体系。

6.3.广泛开设STEM课程，缩小个体计算思维差异

通过之前的调查，不难发现，依旧有一部分的小学生未接触过STEM课程，这可能是由于学生自身感知、教师教学方法所影响，当然，也不能排除是学校未开设STEM课程，或是该类课程仅仅是作为社团课程、兴趣小组活动开展。我们无法保证每一个学生都接受到同样的教育，但是我们可以在力所能及的范围内为学生提供相应的学习条件，STEM课程的开展不一定需要多先进的设备，多完善的场地，例如，“搭建桥梁”这一STEM课程案例，它不受场地限制，不受材料限制，不是一定要用钢筋水泥才能造桥，用木排、纸杯等等的材料也可以完成。因此，不同的地区、学校要因地制宜，尽可能的开设一些STEM课程，为学生提供一条发展计算思维的路径。

参考文献

中华人民共和国教育部制订. (2017). 普通高中信息技术课程标准. 人民教育出版社.

白雪梅, & 顾小清. (2019). K12阶段学生计算思维评价工具构建与应用. 中国电化教育(10).

任友群, 隋丰蔚, & 李锋. (2016). 数字土著何以可能?——也谈计算思维进入中小学信息技术教育的必要性和可能性. 中国电化教育, No.348(01), 1-8.

余胜泉, & 胡翔.STEM教育理念与跨学科整合模式[J].开放教育研究,2015,21（04）:13-22.

董泽华. (2016). 试论我国中小学实施stem课程的困境与对策. 全球教育展望(12), 36-42,62共8页.

Herschbach, D. R. . (2016). The stem initiative: constraints and challenges. Journal of STEM Teacher Education, 48(1), 9-9.

Korkmaz, O. ,  Cakir, R. , &  Ozden, M. Y. . (2017). A validity and reliability study of the computational thinking scales (cts). Computers in Human Behavior, 72(JUL.), 558-569.

Sahin, & Alpaslan. (2015). A practice-based model of stem teaching ||. , 10.1007/978-94-6300-019-2.

Seehorn, Deborah, Carey, Stephen, Fuschetto, & Brian, et al. (2011). CSTA K-12 computer science standards. ACM.

Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35.